This is a transcript-from-memory (what I wish I'd said) of the talk I
just gave at EuroPython 2010, for which I
owe a debt of gratitude to Richard Jones for his last-minute moral
support while wrestling with projectors and refresh rates; and to the
whole team of hard-working volunteers, especially John Pinner & Richard
Taylor, who gave so much time and effort to make EuroPython in the UK
brilliant once again.
The demonstrated code is available at
https://github.com/tartley/gloopy
With this talk I want to give an overview of creating 3D graphics in
OpenGL from Python. Instead of covering topics already covered by a
thousand OpenGL tutorials, I want to shift attention towards some ideas
of how to generate the input to your renderer - how to algorithmically
create geometry. I'll show that with just a paltry few hundred lines of
relatively simple code, you can generate some interestingly chunky
shapes - virtual sculptures, if you will. Since this talk has the word
hobbyist in the title, I want to emphasise how easy this is, and I
want to have some fun with the pretty pictures.
Out of interest, how many people here are already expert OpenGL users
(a few hands hesitantly go up, then some think about it and go down
again) err, I mean how many have already used OpenGL to do anything at
all (about half the people raise their hand.) Alright, well, I want
you all to leave here enthused to go generate your own images or
animations or games.
Inspirations
As the field of computer graphics advances, there's an understandable
tendency for more photorealism, This is laudable, but I also feel that
the effort expended on achieving this technical goal is often undertaken
without considering whether photorealism is the best aesthetic choice
for a particular project.
In the past, games and other applications adopted particular visual
styles out of technical necessity. As is often the case, these
restrictions resulted in a diverse blossoming of creative ideas,
producing an enormous set of distinctive visual styles and experiences.
Crucially, the most successful and memorable examples of these were
projects that found ways to work in harmony with the restrictions of the
medium, rather than attempting to gloss over them.

Advances in computing power and technique provide modern games and
applications with a far wider range of options in how to present
themselves visually, and yet the greater proportion of them seem content
with a conventional and unimaginative 'near-photorealistic' appearance.
This disappoints me, because I feel that projects that opt for a more
highly stylised look, when appropriately chosen, can create a vastly
more striking and memorable artistic experiences. This is true in movies
and all kinds of art.

As an amateur graphics programmer, I don't have large resources nor much
experience to throw at the problem, so my options and my abilities are
limited. But, like a good artist, I believe it should still be possible
to create things that are both strikingly beautiful and highly
functional, either by working with the restrictions of the medium, or by
finding creative ways to exploit or extend them.

In particular, the kind of minimal, clean-lined aesthetic that amateur
OpenGL programs take on by default are useful for their crisp precision,
as charting and visualisation tools. But above that, I love them for
their stark minimalism, their clean lines and homogeneous fields of
colour.

I wish more professional game developers had an incentive to aim for
less conventional aesthetics - whether they be deliberately retro, or
else striking out in some new direction of their own. It's that brave
minority of projects which do this which form my inspiration.
Starting Point
I'm assuming we already have a minimal OpenGL application, that:
- Opens a window
- Provides an OpenGL context for us to render to
- Sets appropriate 3D projection matrix
- Sets the initial modelview matrix state based on the position and
orientation of a 'camera' object
- Calls our empty 'draw' function once per monitor refresh.
This results in a blank screen, at 60fps. Here's a screenshot, so you
can see exactly what it's doing:

I'm using pyglet & PyOpenGL for this, but this isn't important. Any
framework that provides the above abilities, such as PyGame, along with
bindings to OpenGL, will be just fine. Whichever framework you use, this
minimal application might take on the order of about 150 lines of code,
and is covered in countless tutorials all over the web.
From here on in I plan to show (or at least describe) pretty much all of
the code that I add on top of this minimal OpenGL loop.
Goal
To begin with, I'm going to lead you as quickly as I can through a Shape
class, that model 3D shapes, in a way useful for the creation of
geometry, and then a Glyph class that converts these geometries into
arrays for OpenGL. Finally these arrays get passed into a Render class,
which simply calls glDrawElements to render them.
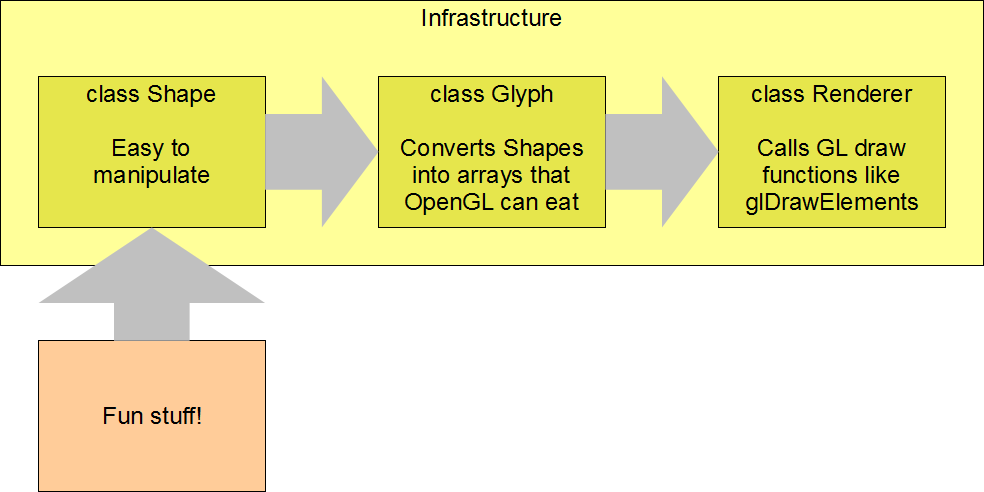
Once the above infrastructure is in place, we can have some fun
generating interesting shapes to make pretty pictures with. The
conventional way to provide geometry to your OpenGL code is by loading
your data from files. Today though, I want to stick with generating
geometry from code, to see where that leads.
Modelling Polyhedra
A polyhedron is a 3D shape with flat faces and straight edges. We can
model coloured polyhedra using a simple Shape class:
Vec3 = namedtuple('Vec3', 'x y z')
Color = namedtuple('Color', 'r g b a')
class Shape(object):
def __init__(self, vertices, faces, face_colors):
# list of Vec3s
self.vertices = vertices
# list of faces, each face is a list of indices into 'vertices'
self.faces = faces
# List of colors, one per face
self.face_colors = face_colors
An instance of this class, for example, might represent a yellow cube,
or a tetrahedron with green and black faces, or any other coloured
polyhedron we can imagine.
To demonstrate how classes Shape, Glyph and Render hang together, let's
examine an even simpler example, a yellow triangle joined to a red
square:
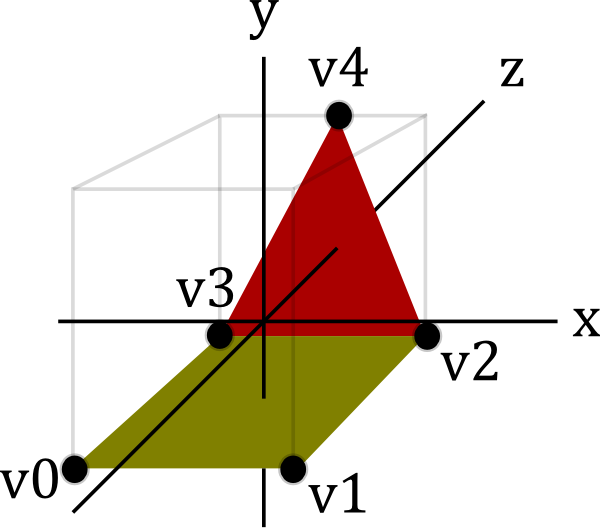
You can see this geometry features five vertices (v0 to v4), which are
used by the two faces. This might be represented by an instance of
Shape:
v0 = Vec3( 1, 1, 0)
v1 = Vec3( 1, -1, 0)
v2 = Vec3(-1, -1, 0)
v3 = Vec3(-1, 1, 0)
v4 = Vec3( 1, 0, 2)
red = Color(255, 0, 0, 255)
yellow = Color(255, 255, 0, 255)
shape = Shape(
vertices=[v0, v1, v2, v3, v4],
faces=[
[2, 3, 4], # f0, triangle
[0, 1, 2, 3], # f1, square
],
face_colors=[red, yellow],
)
The integers in the 'faces' member are indices into the vertices list.
So the triangular face, for example, is formed by linking vertices 2, 3
and 4.
Step 1. Creating a Ctypes Vertex array
In order to render our Shape, we need to convert it to some ctypes
arrays that OpenGL will eat:
- glvertices - an array of GLfloats (three for each vertex)
- glindices - an array of GLubytes (one for each index of each face)
- glcolors - an array of GLubytes (four for each vertex)
To generate glvertices, we need to dereference the indices in
Shape.faces, to produce a new list of vertices, rearranged into the
order they are going to be drawn:
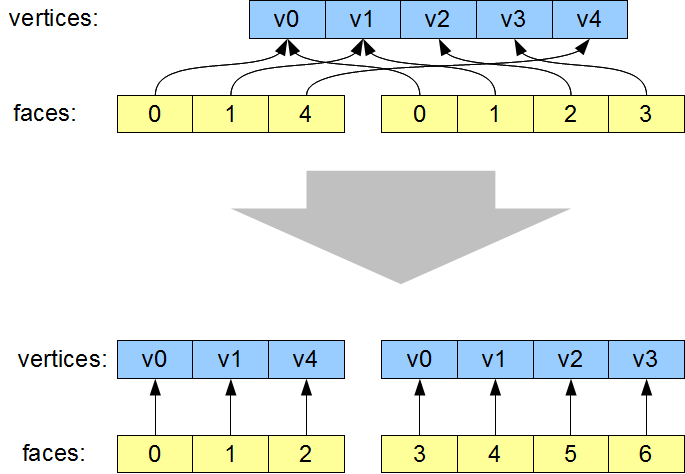
The most visible aspect of this change is that the vertices are
re-ordered, such that the indices now simply read '0, 1, 2, 3, 4, 5...'.
However that isn't actually necessary. The important part of this
transformation is that vertices which are re-used are now duplicated in
the vertex list. For example v0 now occurs twice. As a result of this
vertex duplication, one the two instances of '0' in the faces lists now
instead reads '3' (referencing the new second copy of v0).
This duplication of vertices is required, because when v0 is used for
the first time, it is as part of the red triangle, and when it is used
the second time it is as part of the yellow square. The color of the
vertex changes from one occurrence to the next. All the attributes of a
vertex (position, color, texture co-ords, normals, etc) are treated as
an atomic unit, so whenever any attribute changes, as the color is
changing here, the vertex position needs to be redundantly specified
again, so as to create a new unique vertex with its own unique attribute
values. Even if the color of v0 in our example was identical for each
use, we will see later that other vertex attributes such as surface
normals will still differ. Don't sweat trying to eliminate these
redundancies, they are necessary, unless every single attribute of the
re-used vertex (including surface normals) are identical.
The code in Glyph.get_glverts() performs this dereferencing step:
class Glyph(object):
def get_glverts(self, shape, num_glverts):
glverts = chain.from_iterable(
shape.vertices[index]
for face in shape.faces
for index in face
)
ArrayType = GLfloat * (num_glverts * 3)
return ArrayType(*glverts)
This uses a generator to produce the vertices in the order that we need
them. 'ArrayType' shows the standard idiom to create a ctypes array - we
take the datatype of the array elements, in this case GLfloat since our
vertex positions consist of three floats, and multiply it by the
required length of the array. This yields a new array type. The final
return statement instantiates this array type using the data supplied by
the glverts generator.
Step 2. Creating Ctypes Index Arrays
The second job Glyph has to do is create a ctypes indices array, which
is derived from the Shape's faces. In doing this, it has to break the
Shape's faces down into individual triangles.
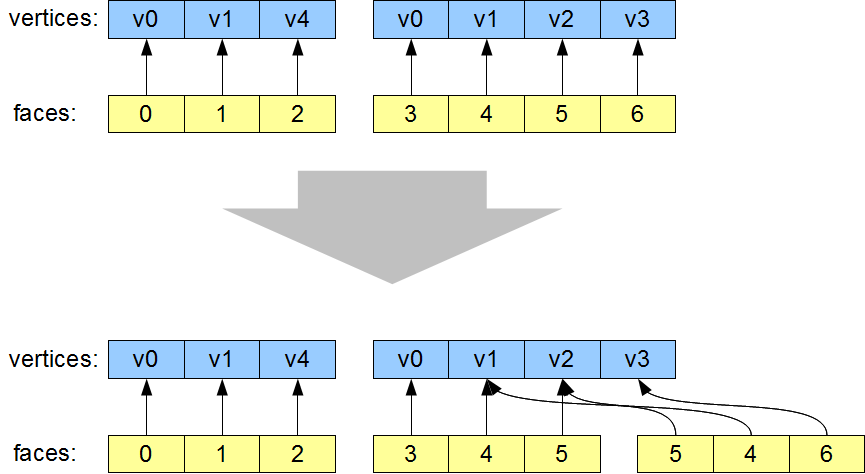
The vertex list is unchanged by this step, and the first face - the
triangle - is also unchanged. The second face, the square, has been
broken into two triangles.
There are well-known algorithms for breaking an arbitrary polygon down
into individual triangles. Using the utility functions found in the GLU
library, this can be done in about 150 lines of Python. But in the
interests of keeping it simple, I decided to restrict our code to just
handling convex faces. Tessellating these faces can be done using a
considerably simpler algorithm:
def tessellate(face):
'''
Break the given face into triangles.
e.g. [0, 1, 2, 3, 4] ->
[[0, 1, 2], [0, 2, 3], [0, 3, 4]]
Does not work on concave faces.
'''
return (
[face[0], face[i], face[i + 1]]
for i in xrange(1, len(face) - 1)
)
We again use a generator, to simply join up the face's first vertex with
all the other vertices, like this:
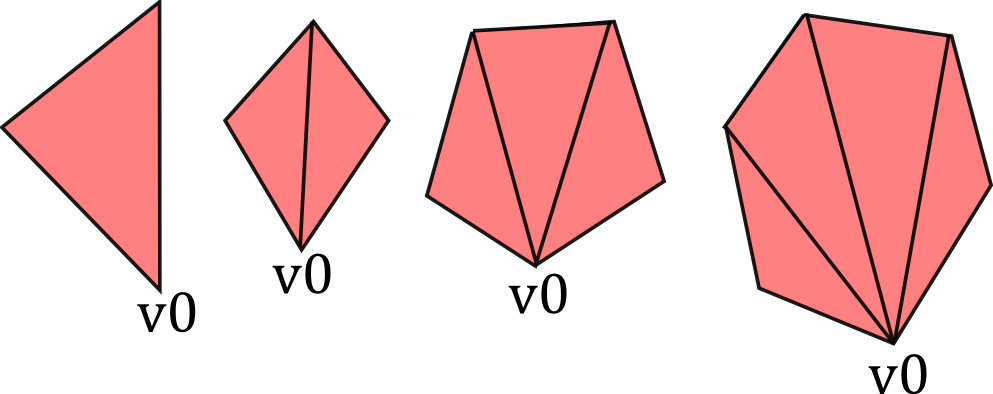
Now we have our tessellate function, Glyph can now create the glindices
array in much the same way as it generated the glvertices. I wasn't
smart enough to write this as a generator first time around, I presume
it would require more than one generator to do it (anyone?), so I'm
needlessly creating an in-memory copy of the sequence, but it turns out
I need to take its length right afterwards anyway, so what the heck:
class Glyph(object):
def get_glindices(self, faces):
glindices = []
face_offset = 0
for face in faces:
indices = xrange(face_offset, face_offset + len(face))
glindices.extend(chain(*tessellate(indices)))
face_offset += len(face)
ArrayType = GLubyte * len(glindices)
return ArrayType(glindices)
This is more complex than get_glvertices because it is performing both
of the transformations described in steps 1 and 2. But it's still pretty
straightforward. Note that the type of the index array will have change
from GLubytes to GLushorts (or GLuints) if the number of vertices rises
above 256 (or 65,536.)
Step 3. Creating Ctypes Color Arrays
Finally, we need an array of vertex colors. This is the simplest of the
lot, generated by repeating the face_color for each face, once per
vertex:
class Glyph(object):
def get_glcolors(self, faces, face_colors, num_glvertices):
glcolors = chain.from_iterable(
repeat(color, len(face))
for face, color in izip(faces, face_colors)
)
ArrayType = GLubyte * (num_glvertices * 4)
return ArrayType(chain(*glcolors))
First Light
It's might seem like a teensy bit of a slog to get here, but it hasn't
been more than sixty lines of code, and now we're in a position to pass
our ctypes arrays into OpenGL's drawElements. This happens in our
Render.draw() method:
class Render(object):
def draw(self, world):
for item in world:
glVertexPointer(3, GL_FLOAT, 0, item.glyph.glvertices)
glColorPointer(4, GL_UNSIGNED_BYTE, 0, item.glyph.glcolors)
# TODO: handle the item's position and orientation
glDrawElements(
GL_TRIANGLES,
len(item.glyph.glindices),
GL_UNSIGNED_BYTE,
item.glyph.glindices
)
This is canonical OpenGL render code, so I'm not going to dissect it,
but now we get some actual visible output:

Hooray! \o/ We can move our camera position around, and view this 3D
object from different angles.
There's a minor wrinkle here that I'm glossing over. I've turned on
backface culling, so the triangle and square aren't visible if we view
them from the back. For all our future examples I plan on using closed
polyhedra, so we won't be able to see the 'backs' of the faces - those
will be on the inside of the polyhedron.
The Fun Stuff
So now we've got all our infrastructure in place, we can start creating
factory functions to churn out some Shapes. Let's start with something
straightforward, a tetrahedron (triangle-based pyramid):
def Tetrahedron(edge, face_colors=None):
size = edge / sqrt(2)/2
vertices = [
(+size, +size, +size),
(-size, -size, +size),
(-size, +size, -size),
(+size, -size, -size),
]
faces = [ [0, 2, 1], [1, 3, 0], [2, 3, 1], [0, 3, 2] ]
return Shape(vertices, faces, face_colors)
Which produces a tetrahedron:

Then a cube factory:
def Cube(edge, face_colors=None):
e2 = edge / 2
verts = list(itertools.product(*repeat([-e2, +e2], 3)))
faces = [
[0, 1, 3, 2], # left
[4, 6, 7, 5], # right
[7, 3, 1, 5], # front
[0, 2, 6, 4], # back
[3, 7, 6, 2], # top
[1, 0, 4, 5], # bottom
]
return Shape(verts, faces, face_colors)
The six faces are quite evident, but the use of itertools.product to
produce the list of vertices perhaps deserves a bit of exposition. It's
an inspired tip from ΤΖΩΤΖΙΟΥ.
Just to spell it out in longhand:
>>> from itertools import repeat, product
>>> list(product(*repeat([-1, +1], 3)))
[(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1),
(1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)]
So there are the eight vertices of the cube, and that gets us the
following:

We can add a few more vertices and faces, to make ourselves a truncated
cube:

Once we've got truncated cubes, we might as well add one last face to
form the entrance:

There's nothing to stop us adding several of these shapes into the world
at once, but since we haven't yet moved any of them away from the
origin, they just sit there, embedded within one another:


Moving objects around
In our earlier Render.draw() method, we left a 'TODO' comment in place,
to note that we weren't yet handling item positions and orientations.
Here's what Render.draw looks like when we fill that code in:
class Render(object):
def draw(self, world):
for item in world:
glVertexPointer(3, GL_FLOAT, 0, item.glyph.glvertices)
glColorPointer(4, GL_UNSIGNED_BYTE, 0, item.glyph.glcolors)
glPushMatrix()
glTranslatef(*item.position)
glMultMatrixf(item.orientation.matrix)
glDrawElements(
GL_TRIANGLES,
len(item.glyph.glindices),
GL_UNSIGNED_BYTE,
item.glyph.glindices
)
glPopMatrix()
Again, this is very standard OpenGL usage. To set an item's position
attribute, I'm going to use a bit of code that I already snuck into the
demo without telling you about. It's the code that moves the camera
around in space. A simplified version is here, class Orbit, which will
return a new position each time it gets called. The locus of this
position is an orbit around the origin:
class Orbit(object):
def __init__(self, distance, speed, phase=None):
self.distance = distance
self.speed = speed
if phase is None:
phase = random.uniform(0, 2 * pi)
self.phase = phase
def __call__(self, time):
bearing = time * self.speed + self.phase
x = self.distance * math.sin(bearing)
z = self.distance * math.cos(bearing)
return Vec3(x, 0, z)
The actual camera uses a slightly longer version I call WobblyOrbit (not
shown), which operates in exactly the same way. Any 'mover' class, i.e.
one that returns a Vec3 position when called, can be used to move the
camera, or any other item, around in space:
class GameItem(object):
def __init__(self, ** kwargs):
self.__dict__.update(** kwargs)
world.add( GameItem(
shape=Cube(1, repeat(red)),
mover=Orbit(distance=20, speed=4),
) )
# then, in world.update():
for item in self.items:
if item.mover:
item.position = item.mover(self.time)
Similarly, we can spin items using 'spinner' classes, that tweak an
item's orientation as time goes by.
With these all in place, we can now add many Shapes to the world, each
moving and rotating independently:

Next week: Composite Shapes...
This is all great as far as it goes, but it turns out we have a
performance problem. Adding more than about 450 shapes at once starts to
slow down below 60fps (This is all on my trusty 2005-era Thinkpad T60
laptop.) The bottleneck turns out to be in our Render.draw() loop. Each
of those OpenGL functions are from (wrappers around) the OpenGL C
library, and calling across the Python / C boundary like this incurs a
per-function call overhead. Also, a second looming problem is that
creating more interesting shapes is going to become more onerous and
error-prone, as we create longer and more complex lists of vertices and
faces in our code.
One partial solution to both these problems is to use composite shapes,
in which we can compose many copies of our basic shapes into one single,
more complex shape. This will allow us to use algorithmic means to
produce more fun geometry, and will also help us draw more complex
shapes, composed of many simpler shapes, without requiring several
separate OpenGL function calls for each of the simple shapes.
On to Part 2 >>




































